统计分析入门

lingxh大约 34 分钟

统计分析入门

作者：https://space.bilibili.com/288965593

1.1 个体、变量与变异

1.1.1 个体

个体是统计分析根据研究目的，所确定的最基本的研究对象单位，所以个体又称为观察单位
- 分析配件日消耗量
- 分析业务人员的维修服务费

1.1.2 变量

根据研究目的确定研究对象
然后对研究对象的某项目或与研究指标进行观察（或测量）
这种观察项目或研究指标称为**变量**（variable）

1.1.3 变异

同质个体的某指标（变量）值的差异称为个体变异（individual variation）
- 统计学就是研究变异规律的学科，不存在变异的问题不属于统计学的研究范畴。或者说，正是因为存在变异，才有了统计学的用武之地
- 所以，对于无变异的常量问题，或者严格的数学函数问题，并非统计学的应用领域

1.2 变量类型

1.2.1 连续变量（continuous variable）

连续变量的取值范围是一个区间，它可以在该区间中连续取值，即连续变量可以取到区间中的任一值，并且一般有度量单位
- 因此有的统计书中将其称为区间变量
- 例：身高、年龄、体重、金额
一些特殊的变量并不能渠道任意值，但仍然按照连续变量处理
- 例：班级学生总数、配件消耗量

1.2.2 离散型变量（discrete variable）

取值范围是有限个值或者一个数列构成的，表示分类情况的离散型变量又称为分类变量
根据类别的有序性，分类变量可以分为
- 有序变量
  - 例：收入级别、售后服务满意度（满意、一般、不满）
- 无序变量
  - 血型、民族
二分类为很特殊的一类，无所谓次序问题

1.2.3 变量类型：总结

连续变量：有大小之分，各取值之间间距明确
有序分类变量：有大小之分，但是各类别间的间距大小不明
无序分类变量：无大小之分，仅知道属于不同类别

1.3 数据类型的转换

连续变量、有序变量、无序变量间的信息量越来越少，在丢弃一部分信息量的前提下，可以将变量向信息量减少的方向加以转换
连续数据与分类有序数据
- 人为划分级别
- 例：年龄->划分为少年、青年、中年、老年
有序分类数据与两分类数据
- 按照某个级别一分为二
- 例：年龄->划分为小孩、成人
问题：逆向转换是否可行
- 例：优、良、中、差变为1、2、3、4

1.4 总体、样本与随机抽样

1.4.1 总体

总体（population）是根据研究目的确定的同质所有个体某指标观察值（测量值）的集合
- 有限总体（finite population）和无限总体（infinite population）

1.4.2 样本

在一个较大范围的研究对象中随机抽出一部分个体进行观察或测量，这些个体的测量值构成的集合称为样本（sample）
- 大多数统计研究都只能接触到样本
- 例：配件故障率只能通过样本来获取

1.4.3 随机抽样

在抽样研究中，随机抽出的一部分个体进行观察或测量的过程称为随机抽样（random sampling）
- 随机抽样的本质：每个个体最终是否入选在抽样进行前是不可知的，但是其入选可能性是确切可知的（多数情况下为等概率）
- 注意：随机≠随便

1.5 统计量、总体参数与抽样误差

1.5.1 统计量

刻画样本特征的统计指标称为统计量（statistic）
- 例：样本的平均值

1.5.2 总体参数

刻画总体特征的指标称为总体参数（parameter）
- 例：总体中某个指标的所有个体变量值的平均数称为总体均数
- 统计研究中真正希望加以研究考察的都是总体参数，但参数一般是无法直接求得的，只能从统计量的大小加以推估

1.5.3 抽样误差

许多总体指标是未知的，需要用相应的样本统计量对其进行估计。由随机抽样造成的样本统计量与总体指标之间的差异称为抽样误差（sampling error）
虽然在一次抽样研究中的抽样误差大小是堆积的，但抽样误差在概率意义下有规律可循，这种规律称为抽样分布

1.6 频率、概率与小概率事件

1.6.1 频率

随机事件：随机现象某个可能的观察结果称为一个随机事件
- 例：投一枚硬币出现正面（或反面）
频率（frequency）：观察到的随机事件某个结局的出现频次（比例），可以被直接观察到
- 例：投10次硬币5次为正面

1.6.2 概率

概率（probability）：概率刻画随机事件发生可能性大小，其取值介于0和1之间
- 不能直接观察到，但可以通过频率估计，试验次数越多，估计越精确

1.6.3 小概率事件

在统计学中，如果随机事件发生的概率小于或等于0.05，则认为是一个小概率事件，表示该事件在大多数情况下不会发生
一般认为小概率事假在一次随机抽样中不会发生，这就是小概率原理
小概率原理是统计推断的基础
- 经典的小概率事件：瞎猫碰上死耗子

1.7 统计研究的步骤

设计、收集、整理、分析

1.7.1 设计

设计：全过程最关键的一步，良好的开端是成功的一半，这也是最考察统计科研能力的步骤
选题--明确研究目的--提出假设--明确总体范围--确立观察指标--控制研究中的偏倚--给出具体的研究方案

1.7.2 收集

收集：最两级分化的步骤
- 质量控制极端重要
- Garbage in，Garbage out

1.7.3 整理

整理：越来越倾向于半自动化，有许多软件工具可用，但这并不意味着该过程不重要

1.7.4 分析

统计描述：了解样本数据的情况，是全部工作的基础，是尽量精确、直观而全面的对所获得的样本进行呈现
- 为了达到这一目的，需要使用一系列专门的统计描述指标
- 这些指标的呈现方式又可分为两种
  - 统计图：直观，但精确度稍差
  - 统计报表：能尽量详细，精确，但不够直观
统计推断：从样本信息外推到总体，以最终或的对所感兴趣问题的解答
- 参数估计：样本--所在总体特征
  - 例：该配件的日平均用量是多少
  - 用样本的平均值表示总体的平均值
- 假设检验：该指标可能的影响因素分析
  - 例：和晴天相比，雨天的配件用量是否更低

2.统计描述

2.1 连续变量和分类变量的统计描述

2.1.1 频数表

是一种非常直观的方法，但是比较粗糙
- 确定组数：组数不宜过多，但也不能太少，保证大多数组都有数个观察值
- 确定组距：在确定了全距后，一般进行灯等距分组
  - 组距≈极差/组数
- 确定各组段的上下限
  - 各组的起点被称为该组的下限，终点被称为上限

2.1.2 从频数图/表中可获得的信息

集中趋势
- 高峰组段在什么位置出现
离散趋势
- 数据的分布范围是什么，分散程度如何
分布形状
- 是否堆成，分布曲线的形状
- 正、负偏态和左右偏
  - 大头在坐标轴左边为正偏态（右偏）
分布特征
- 单、双峰，有无极端值等

2.1.3 进一步的统计描述指标

通过对频数表/频数图的观察，研究者可以得到上述各方面信息的一个大体印象
但是，如果希望进行深入的分析，则必须要使用一些更为严谨，准确地统计指标对上述各方面特征加以描述
什么时候不一定需要用这些统计描述指标
- 所研究的总体中个体数很少且在样本中都已出现时
- 例：了解北京、上海、广州这三个特级城市2012年人口数，只有三个数据点

2.2 集中趋势的描述指标（Central tendency）

2.2.1 均数

2.2.1.1 均数

均数 Mean
- 描述一组数据在数量上的平均水平，总体均数和样本均数分别用不同符号表示 $\mu和\bar{X}$
注意：均数在书写上应当带有和原始测量值相同的测量单位
均数的实质：把总体各单位的差异全部抽象化，采用取长补短的方法把变量值小于平均数的负离差全部用大于平均数的正离差抵消补齐

2.2.1.2 均数的优点

高度浓缩了数据的精华，是大量的观测数据转变为一个代表性数值
数据资料中任何频次、次序和数值大小的变化，都会引起平均数的改变。因此它是灵敏的，也是对资料所提供信息运用的最为充分的

2.2.1.3 均数的缺点

大锅饭：把各个观测数据之间的差异性掩盖了起来，这不一定合适
欺骗性：由于平均数对个别极端值的反应比较灵敏，因而均数在某些情况下可能具有一定的欺骗性

2.2.1.4 均数的适用范围

对称分布资料，特别是正态分布资料

2.2.2 中位数

2.2.2.1 中位数

中位数 Median
- 是将全体数据按大小顺序排列，在整个数列中处于中间位置的那个值。它把全部数值分成两部分，比它小和比它大的数值个数正好相等
- 中位数作为分布数列中处于中等水平的代表值，能够将全部总体单位按数值的大小分成两个部分。所以中位数又称为二分位数
- 代表符号：M

2.2.2.2 中位数的优点

它是位置平均数，不受极端值的影响，在具有个别极大或绩效值的分布数列中，中位数比算数平均数更具有代表性

2.2.2.3 中位数的缺点

损失信息：由于中位数只考虑居中位置，其它变量值比中位数大多少或小多少，它是无法反映出来的。所以，用中位数会损失很多信息
不稳定：当样本量较小是，中位数会不太稳定，并不是一个好选择

2.2.3 几何均数

几何均数 Geometric mean
- 在医学、化学研究中经常会遇到一种特殊的资料，其数值呈等比方式记录，本身为正偏态分布，但是如果进行对数变换，则变换后的数据呈正态分布
- 为了能够充分利用数据信息，可以考虑先进行对数变换，然后求得此时的算数平均数，最后将该均数反对数变换回来，这就是所谓的几何均数
- 表示符号：G

2.2.4 众数

2.2.5 截尾均数

有些数据在开头和结尾出会有极端值，通过删除这部分数据后的数据所得的均数
一般各自删除前后5%

2.3 离散趋势的描述指标 Dispersion tendency

2.3.1 全距

全距 Range
- 优点
  - 容易理解
  - 使用范围最广
- 缺点
  - 不稳定

2.3.2 方差

方差 Variance $\sigma^2 = \sum{(x-\mu)^2}/n$

2.3.3 标准差

标准差 std.deviation
- 解决了量纲问题
- 注意：deviation指的是偏离程度，而不是错误程度

\sigma = \sqrt{\sum{(x-\mu)^2}/n}

对于样本来说，标准差为

S = \sqrt{\sum{(x-\bar{X})^2}/(n-1)}

2.3.4 变异系数

变异系数 Coefficient of Variation

CV = S/\bar{X}

解决了不同资料间变异程度对比的问题

2.3.5 方差-标准差-变异系数的使用范围

以均数为集中趋势代表值，因此使用范围也受到相应的限制
本质上只适用于正态分布资料

2.3.6 百分位数

百分位数
- 是一种位置指标，用Px表示。一个百分位数Px将一组观察值分为两部分，理论上有x%的观察值比它小，还有（100-x）%的观察值比它大

2.3.7 四分位数

四分位数
- 即P25、P50、P75分位数的总称
- 正好将样本值四等分，且P25和P75中间包括了50%的观察值，因此四分位间距既排除了两侧极端值的影响，又能够反映较多数据的离散程度

2.3.8 分布形状描述指标

分布形状描述指标 Distribution
- 针对某种分布进行进一步的特征描述，常见的是用于正态分布的两个两个指标
  - 偏度系数 Skewness 正态峰正偏态负偏态
  - 峰度系数 Kurtosis 正态峰平阔峰尖峭峰
其他指标
- 离群值与极端值列表

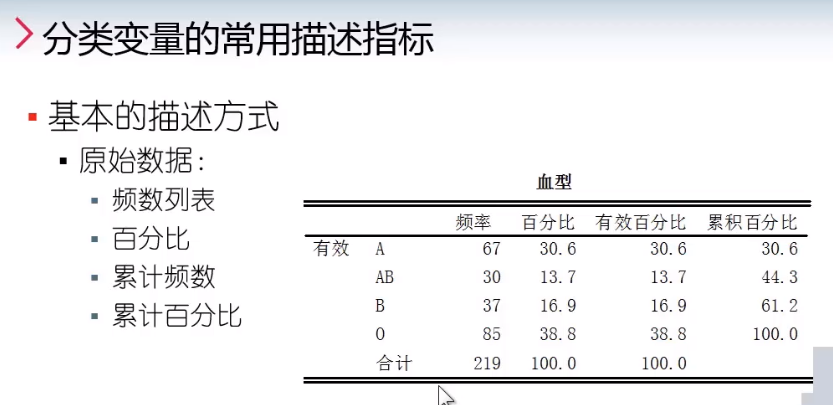
2.4 分类变量的常用描述指标

基本的描述方式
- 原始数据
  - 频数列表
  - 百分比
  - 累计频数
  - 累计百分比

2.4.1 比

比（ratio）
- 任意两个变量之比，这两个变量可以是性质相同的两个指标，如两个地区相同时间内某病新发病例数之比；也可以是性质不相同的两个指标之bi
  - 性别比，货物/销售人员比，人口密度等
  - 两者的比值必须有专业意义
构成比（proportion）
- 部分占总体的比例，分为k个部分（A1、…、Ak），其中某一个部分观察对象与观察对象总数之比为构成比
  - 构成比的分子是分母的一部分，所以其取值必在0与1之间，各部分的构成比之和应当为1

2.4.2 率

率（rate）
- 某个时期内某个事件发生的频率或强度，是一个具有时间概念的比，实际上可以和物理中率的定义相对照

率= \frac{某时期内发生某事件观察单位数}{该时期开始时暴露的观察单位}

按上式，率的分子也应是分母的一部分，故其取值应在0到1之间变动

3.统计推断

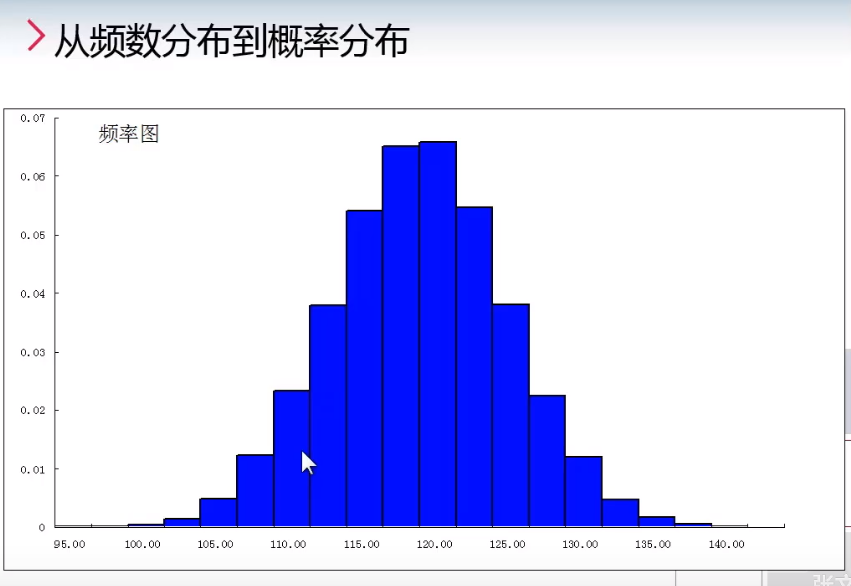
3.1 从频率分布到概率分布

直方图/频率图的性质
- 直条的面积实质上就是频率（或者百分比）
  - 面积 = 高度（频率/组距）*宽度（组距）= 频率
- 所有直条面积相加等于1
  - 当样本量越来越大，频率（面积）趋向概率
  - 并且组距越来越小是，直方条的顶缩成点并且各个直方条的顶连接成一条曲线，这条曲线就是概率密度分布曲线
  - 概率密度的概念和固体的密度基本相似
- 所以概率密度曲线下的面积就是相应的累计概率
- 概率密度曲线就是大量重复随机变异的规律

3.2 正态分布

正态分布的两个重要特征：均数μ和标准差σ
- 记为 $X~N(\mu,{\sigma}^2)$
- μ是分布曲线的峰位置（集中趋势）
  - 又被称为位置参数
- σ大离散程度大，σ小离散程度小（离散趋势）
  - 又被称为形状参数
- 正态分布的对称性

3.3 标准正态分布

标准正态分布N（0,1）和其他正态分布 $N(\mu,{\sigma}^2)$ 的关系

如果X~N(\mu,{\sigma}^2)，则y = \frac{X-\mu}{\sigma}~N(0,1)

标准正态分布的曲线下面积分布规律
95% 99%
双侧 1.96 2.58
单侧 1.64 2.33
因此，只要将相应的指标转换为服从标准正态分布，就可以根据该面积分布规律计算出累积概率
- 例：95%的双侧个体参考值范围

	95%	99%
双侧	1.96	2.58
单侧	1.64	2.33

(\bar{X}-1.96\sigma,\bar{X}+1.96\sigma)

3.4 二项分布

3.4.1 基本概念

注意：两分类变量并非一定会服从二项分布
Bernoulli试验（伯努利）
- 例：袋子里有5只乒乓球，2黄3白。每次摸1球，放回再摸。摸100次，摸到黄球的次数为…
- 对每一次实验，出现的结果只有两种情况，称为Bernoulli试验。如所关心的事件A发生，称为“成功”，否则称为失败，每次试验结果，只能是两个互斥的结果之一
Bernioulli试验序列
- 在重复试验中，如果对每一次实验，出现的结果只有两种情况，即Bernoulli试验。
- 每次试验的条件不变。即每次试验中，结果A发生的概率不变（均设为pi）
- 各次试验独立。即一次试验出现什么样的结果与前面已出现的结果无关
- 由满足以上三个条件的n次Bernoulli试验构成的序列被称为Bernoulli试验序列
对于Bernoulli试验序列的n次试验，结局A出现的次数X的概率分布服从二项分布
- 二项分布指的是概率的分布
- 注意：二项分布是一个离散型分布
- 其取值概率为

P(X=K)=\tbinom{n}{k}\pi^k(1-\pi)^{n-k}

3.4.2 二项分布的基本特征

显然对于不同的n，不同的pi有不同的二项分布。它们是二项分布的两个参数
若X服从二项分布，则记为X~B(n,pi)

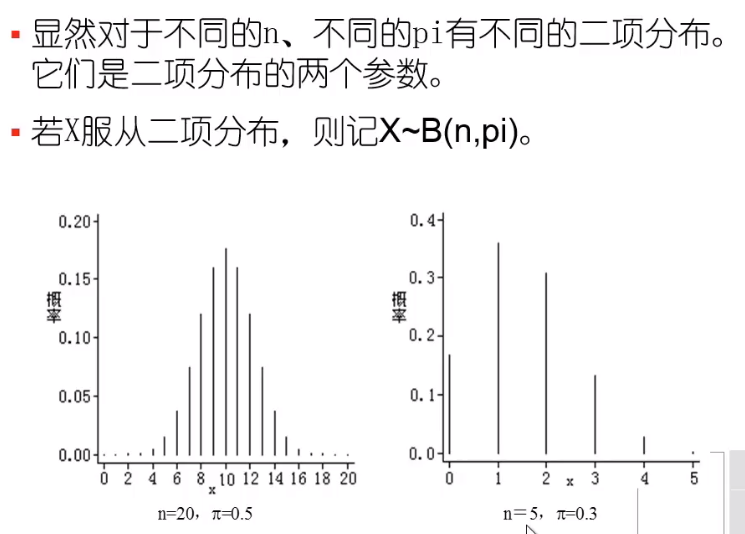
二项分布的均数和方差
- μ=n*pi
- 方差=n*pi*(1-pi)
当pi=0.5时，图形对称；当pi≠0.5时，图形呈偏态，但随n的增大，图形逐渐对称
因此，当n较大，pi不太极端时，可以采用正态近似方法计算概率分布规律

3.5 统计推断

统计推断
- 统计推断，或者说统计估计，就是根据你拥有的信息来对现实世界进行某种判断
- 从数据得到关于现实世界的结论的过程就叫做统计推断（statistical inference）
重要提示：任何一个总体参数都可以进行统计推断
- 例：配件日消耗量的均数、中位数、标准差、四分位数间距、变异系数等等，都是可以进行统计推断的

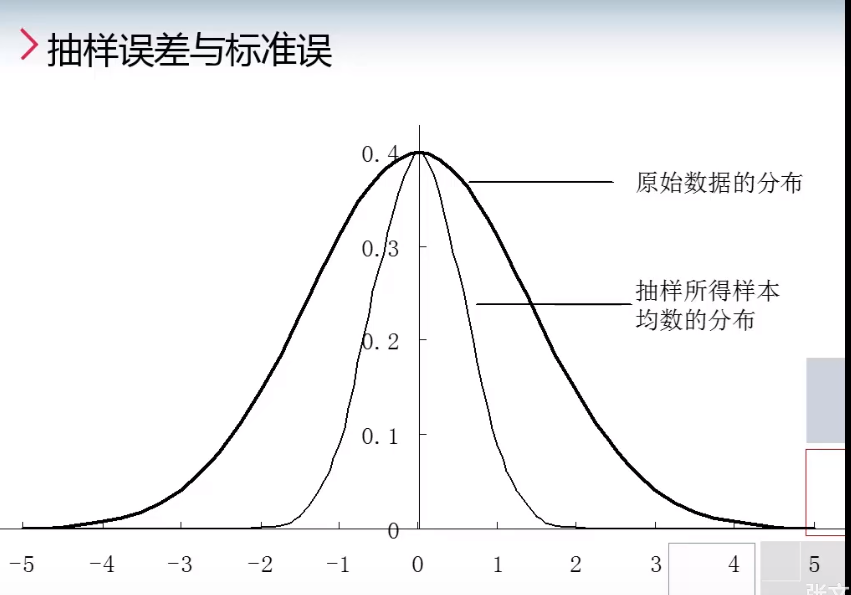
3.6 抽样误差与标准误

样本指标存在着变异/抽样误差

3.6.1 抽样误差

抽样误差
- 抽样误差：由抽样导致的样本均数与相应总体均数在数值上的差异
  - 如何定量表达其大小、
  - 样本均数与真是总体均数之差看上去是可以表示抽样误差大小的，但实际上无法计算
- 考虑在一个总体中实际上可进行无限多次抽样，实际上这些样本的抽样误差应当也服从某种分布规律
样本均数存在随机变异，但在大量重复观察的情况下，可以证明同样有一定的规律，即：样本均数的概率分布
样本均数服从 $N(\mu,\sigma^2/n)$ ,样本均数的抽样误差是随机的，因此也有相应的规律（概率密度曲线 $N(0,\sigma^2/n)$

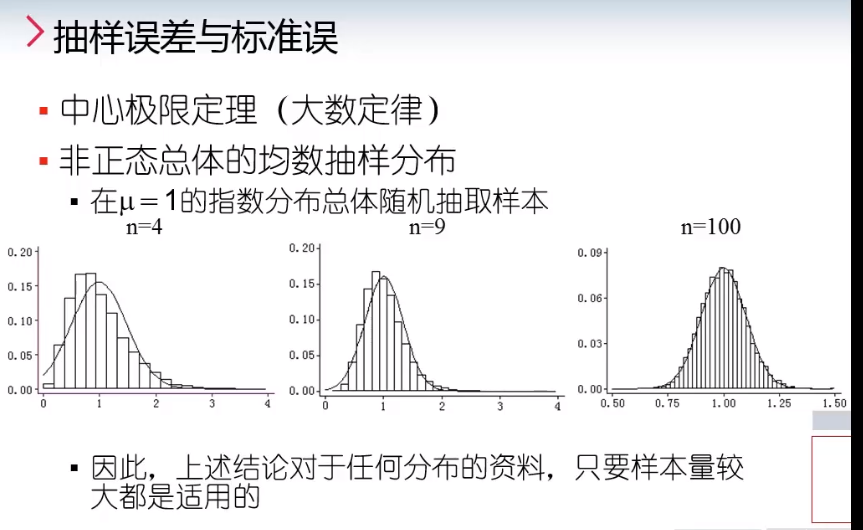
3.6.2 中心极限定理

中心极限定理（大数定律）
- 非正态总体的均数抽样分布
  - 在μ=1的指数分布总体随机抽取样本

3.6.3 标准误

标准误
- 样本均数服从 $N(\mu,\sigma^2/n)$ 中，其方差的平方根同样是标准差（标准偏差），只是该标准差表示的是样本均数抽样误差离散程度大小
- 因此又被称为样本均数的标准误（Std.error，标准误差，代表错误的大小）
$\sigma_{bar{X}}=\frac{资料X的总体标准差\sigma}{\sqrt{n}}$

3.6.4 影响抽样误差的因素

总体内各个体间的变异程度
样本含量N的大小

3.6.5 t分布

由于在实际研究中，我们往往无法得知总体标准差σ，但是可以用样本标准差S估计，从而均数标准误的估计公式为
$S_{\bar{X}}=\frac{S}{\sqrt{n}}$
如果使用总体标准差进行计算，则
$\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$
服从标准正态分布
但由于一般只能使用样本标准差进行估计，则
$\frac{\bar{X}-\mu}{S/\sqrt{n}}$
服从的是t分布
自由度：样本数值可以自由取值的个数

3.6.5.1 t分布

t分布
- 英国统计学家W.S.Gosset（1908）给出了统计量t的分布规律，并称统计量
  $t=\frac{\bar{X}-\mu}{S/\sqrt{n}}\cdots v=n-1$
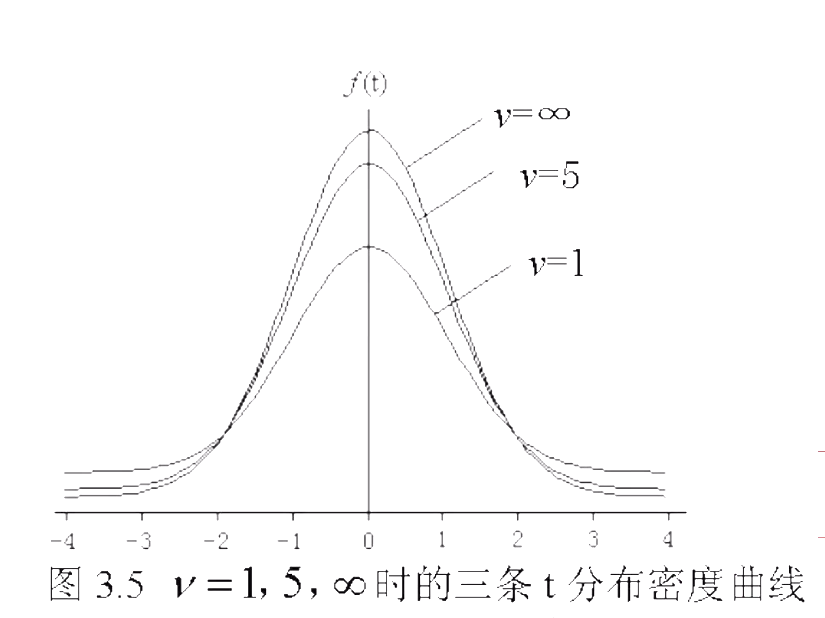
  的分布规律为t分布，自由度为v，记为t(v)分布
- 由于每个自由度v对应一个分布，因此t分布式一簇分布而不是一个分布

3.6.5.2 t分布的图形特征和t界值

t分布的图形特征
- t分布曲线是关于t=0对称的单峰曲线
- 自由度v较小是，t分布于标准正态分布相差较大，并且t分布曲线的尾部面积大于标准正态分布曲线的尾部面积
- 当自由度无限增大是，t分布逼近于标准正态分布
t分布的t界值
- 给定自由度v，t分布曲线下面积有分布规律
- 统计学家为此编制了t界值表

3.6.5.3 样本率的抽样分布

对于大量重复随机抽样而言，样本率p同样会围绕着总体率波动，样本量n的值越大，这种波动就越小
当n的值比较大是，p的分布就近似于均数为pi，标准差为sqrt(pi*(1-pi)/n)的正态分布
- 一般的标准是n*pi和n*(1-pi)均大于5，且n>40
- 当样本情况接近此标准是，往往会进行校正
- 这里所说的样本率的标准差反映的就是抽样误差的大小，所以一般有称为阳性数x的标准误

3.7 参数估计

3.7.1 推断方法

推断方法：点估计与区间估计
- 点估计：样本均数直接作为总体均数的点估计，但显然仅有点估计是不够的
- 区间估计：根据相应标准误的大小，按照一定的可信度给出一个总体参数可能的取值范围
  - 该区间被称为可信区间

3.7.2 可信区间的计算

已知 $U=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$
则根据标准正态分布的面积规律，应当有95%的样本均数在以下范围内
$-1.96<\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}<1.96$ $变换后\cdots \bar{X}-1.96\sigma/\sqrt{n}<\mu<\bar{X}+1.96\sigma/\sqrt{n}$
该表达式被称为总体均数的95%可信区间
当使用S代替σ计算时，由于变换后的统计量服从的是t分布，因此相应的95%界值也按照t分布界值来给出，而不再是1.96
$\bar{X}-t_{v/2}S/\sqrt{n}<\mu<\bar{X}+t_{v/2}S/\sqrt{n}$

3.7.3 可信区间的含义

可信度仅仅是大量重复抽样时的一个渐进概念
计算出的区间是固定的，而总体参数值也是固定的
因此，只有两种可能：包含或不包含，这当中没有任何概率可言
95%的可信度只是说如果我们能够大量重复试验的话，则平均下来每100个可信区间中，会有大约95个覆盖真实值

4.常用假设检验方法

4.1 为什么要做检验

从统计描述结果中发现可能的数据规律
但如果是抽样研究的样本，此时获取的只是样本的信息
研究者关心的并不仅仅是与样本，更希望了解相应的总体特征
- 参数估计：推估样本所在的总体特征
- 假设检验：对提出的一些总体假设进行分析判断，做出统计决策
运用统计知识根据研究设计和资料的性质正确选择分析过程
初步的统计描述（集中趋势、离散趋势）和统计分析
- 集中趋势：均数、P50
- 离散趋势：标准差/方差、四分位数间距
- 分布特征
- 异常值及其他

4.2 假设检验原理

现有的样本均数和已知总体均数不同，其差别可能有两个方面原因造成
- 现有差别为样本的抽样误差
- 样本所来自的总体与已知总体不同，存在本质差异
假设检验原理
基础：小概率原理，即认为小概率事件在一次随机抽样中不会发生
- 最经典的小概率事件：瞎猫碰到死耗子
基本思想：先建立一个关于样本所属总体的假设，考察在假设条件下随机样本的特征信息是否属于小概率事件，若为小概率事件，则怀疑假设成立有悖于该样本所提供的特征信息，因此拒绝假设

4.3 假设检验的基本步骤

4.3.1 建立假设

根据统计推断的目的而提出的对总体特征的假设
统计学中的假设有两方面的内容：
- 检验假设（hypothesis to be tested）：又称原假设或无效假设（null hypothesis），记为 $H_0$
- 备择假设（alternative hypothesis）：记为 $H_1$ 。与 $H_0$ 相对立，意义在于当 $H_0$ 被拒绝时供采用。两者是互斥的，非此即彼
- $H_0:\mu=\mu_0,H_1:\mu\neq\mu_0$
- $H_0:\mu=60g,H_1:\mu\neq60g$

4.3.2 确定检验水准

实际上就是确定拒绝 $H_0$ 时的最大允许误差的概率
检验水准（size of test）：常用 $\alpha$ 表示，是指检验假设 $H_0$ 本来成立，却根据样本信息拒绝 $H_0$ 的可能性大小，换言之， $\alpha$ 是拒绝了实际上成立的 $H_0$ 的概率
常用的检验水准为== $\alpha=0.05$ $α = 0.05$ ==
- 其意义是：在所设 $H_0$ 的总体中随机抽得一个样本，其均数比现有样本均数更偏离总体均属的概率不超过5%
- 类似于考试中习惯用60分作为及格线

4.3.3 计算统计量和P值

实际上在此之前还有一步叫做进行试验，样本数据即从此来
统计量只是工具，概率值才是目的，它可以客观衡量样本对假设总体偏离程度
- 从 $H_0$ 假设的总体中抽出现有样本（及更极端的情况）的概率，即P值
例：600次赢100次是 $H_0$ 假设的情况，只赢1次就是现有样本情况
- 更极端的情况是1次都没有赢
- 以及居然赢了400多次这类更罕见的情况
检验统计量的特点
- 该统计量应当服从某种已知分布，从而可以计算出P值
- 各种检验方法多利用的分布即计算原理不同，从而检验统计量也不同

4.3.4 得出推断结论

按照事先确定的检验水准 $\alpha$ 界定上面得到的P值，并按小概率原理认定对 $H_0$ 的取舍，作出推断结论
若 $P\le\alpha$
- 基于 $H_0$ 假设的总体情况出现了小概率事件
- 则拒绝 $H_0$ ，接受 $H_1$ ，可以认为样本与总体的差别不仅仅是抽样误差造成的，可能存在本质上的差别，属“非偶然的（significant）”，因此，可以认为两者的差别有统计学意义
- 进一步根据样本信息引申，得出实用性的结论
若 $P\ge\alpha$
- 基于 $H_0$ 出现了很常见的事件
- 则样本与总体间的差别尚不能排除纯粹由抽样误差造成，可能的确存在“偶然的（non-significant）”，故尚不能拒绝 $H_0$
- 因此，认为两者的差别无统计学意义，但这并不意味着可以接受 $H_0$ $H_{0}$
  - 尚不能认为有罪 $\ne$ 可确认无罪

4.3.5 关于掷骰子的假设检验

建立假设
- $H_0：筛选均匀，\pi=1/6\cdots H_1:筛子不均匀$
确定检验水准
- $\alpha=0.05$
进行试验，计算检验统计量和P值
- 相应的试验结果在 $H_0$ 下对于对应的概率为1/600略多一点
得出推断结论
- 基于 $H_0$ 出现了小概率事件，结果有非常显著的统计学意义，你出老千！

4.4 一型错误、二型错误和检验效能

	拒绝 $H_0$ ，接受 $H_1$	不拒绝 $H_0$
$H_0$ 真实	Ⅰ型错误 $(\alpha)$	正确推断 $(1-\alpha)$
$H_0$ 不真实	正确推断 $(1-\beta)$	Ⅱ型错误 $(\beta)$

检验效能
- $H_1$ $H_{1}$ 是真的，实际拒绝 $H_0$ $H_{0}$ 的概率为 $(1-\beta)$ $(1 - β)$ ，称为Power，又称为检验效能
  - 由于两种可能的结论中，往往希望得到的是拒绝 $H_0$ 的结论，所以实际问题在分析师检验效能不应当太低
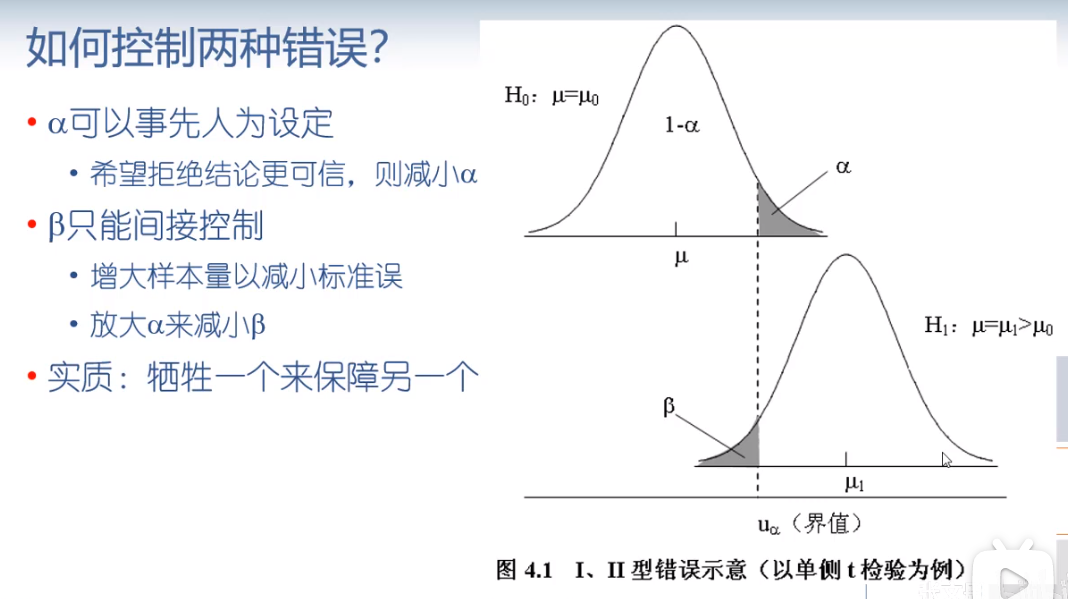
如何控制两种错误
- $\alpha$ $α$ 可以事先认为设定
  - 希望拒绝结论更可信，则减小 $\alpha$
- $\beta$ $β$ 只能间接控制
  - 增大样本量以减少标准误
  - 放大 $\alpha$ 来减小 $\beta$
- 实质：牺牲一个来保障另一个

4.5 假设检验的注意事项

假设检验的单侧和双侧问题
- 双侧检验
  - 不知道样本所在总体和假定总体的相应指标谁高谁低
  - 得到拒绝结论更困难，因此相应得到结果也更稳妥
- 单侧检验
  - 在专业上可知所在总体的相应指标不可能更高/更低于假定总体值
  - 单侧检验更为敏感，但设定单侧检验需要有充分的专业知识来支撑
统计方法应当注意其适用条件
- 独立性（independence）：各观察值间相互独立，不能互相影响
- 正态性（normality）：理论上要求样本取自正态总体
- 方差齐性（homogeneity）：两样本所对应的总体方差相等
假设检验按的结论不能绝对化
- 本身就保留了犯错误的可能性
- 样本量导致的检验效能问题
  - 样本量太小，导致检验效能不足，从而无法检出可能存在的差异
  - 样本量太大，得出的有统计学意义的结论可能根本没有实际意义

4.6 单样本t检验的基本原理

用于连续变量
CCSS项目基期的信息指数数值被设定为100，但这是全部城市的平均水平，请考察基期时广州信心指数均值是否和基准值有差异
推断样本是否来自某已知总体，即要检验样本所在的总体的均数是否等于已知的总体均数
为了回答该问题，统计学上采用了小概率反证法的原理：我们有了一下两种假设
- $H_0$ ：样本均数与（假定的）总体均数的差异完全是抽样误差造成的
- $H_1$ ：样本均数与总体均数的差异除由抽样误差造成外，也反映了两个总体均数确实存在差异

t = \frac{\bar{X} - \mu_0}{S_{\bar{X}}}

先假设 $H_0$ 成立，即一切都是抽样误差造成的。在这个前提下，现有的样本是从已知均数的大总体中抽出来的
显然，样本均数和假设总体均数之差就代表了偏离假设的程度
但此差异所对应的概率究竟是大还是小？仅看这一个数字很难做出判断。因为这还和数据的离散程度有关，为此需要找到某种方式和这一差值进行标准化
标准化的基本方式就是将差值除以表示样本均数离散程度的指标
- 在单样本的情况下，样本的均数服从t分布
这个被标准化的差值，就是本次检验中所谓的统计量
- 由于该统计量服从t分布，可利用该分布得到相应的概率值，故而此处的方法被称为单样本t检验
最终求得的P值表示从假设总体中抽出当前样本均数（及更计算情况）的概率总和
- 如果该P值太小，成为了我们所定义的小概率事件（小于等于 $\alpha$ $α$ 水准），则我们怀疑所做的假设不成立，从而拒绝 $H_0$ $H_{0}$
  - 基本信念：小概率事件在一次实验中不可能发生
- 反之，我们就不能拒绝 $H_0$ $H_{0}$ ，但一般也不太好说去接受它
  - 尚不能认定有罪 $\ne$ 可确认无罪
单样本t检验的适用条件
- 因为有中心极限定理，一般均数的抽样分布都不会有问题，真正会限制该方法适用的是均数是否能够代表相应数据的集中趋势
  - 强烈偏态分布时，均数已经无法正确代表数据的集中趋势
- 也就是说，只要数据分布不是强烈的偏态，一般而言单样本t检验都是适用的

4.7 两样本t检验的基本原理

分析的目的与假设
- 目的：推断两个样本是否来自相同的总体，更具体的说，是要检验两样本所代表的总体均数是否相等
  - 当数据服从正态分布时，总体只需要两个参数就可以确定

t=\frac{\bar{X_1}-\bar{X_2}}{S_{\bar{X_1}-\bar{X_2}}}

基本原理
- 其基本原理与单样本t检验相同
- 首先假设 $H_0$ ：两样本来自同一总体
- 当该总体服从正态分布时，就可以采用两样本t检验来计算从该总体中抽得这样两个样本（及更加极端情况）的概率为多少，从而做出统计推断
适用条件
- 由于 $H_0$ $H_{0}$ 假设的是两样本来自同一总体，分析目的值涉及到均值，因此两样本t检验在推导过程中除了要求总体服从正态分布外，还要求两样本各自所在总体方差相同
  - 独立性：对结果的影响较大，但是一般没问题
  - 正态性：有一定的耐受力，可以通过直方图等进行观察
    - 注意应当要分组考察
  - 方差齐性：相对而言对结论的影响较大，需要进行方差齐性检验
适用条件不被满足时的处理方式
- 情况较轻时可以采用校正t检验的结果
- 否则应使用变量变换使之满足条件
- 或采用
  - 非参数检验方法
  - 贝叶斯推断方法
  - 计算统计学方法（Bootstrap抽样等）

4.8 卡方检验的基本原理

$X^2$ 检验是用途很广的一种方法，主要用于分类数据的统计推断
- 分类资料的分布是否符合假设
- 两个率或两个构成比比较的卡方检验
- 多个率或多个构成比比较的卡方检验
- 分类资料的相关分析
- 模型是否和样本数据完美拟合
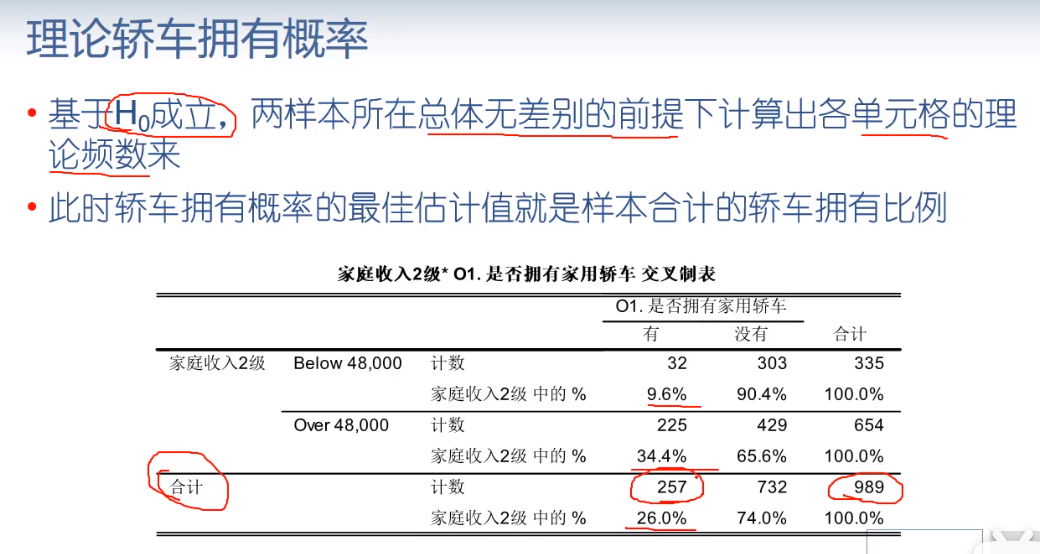
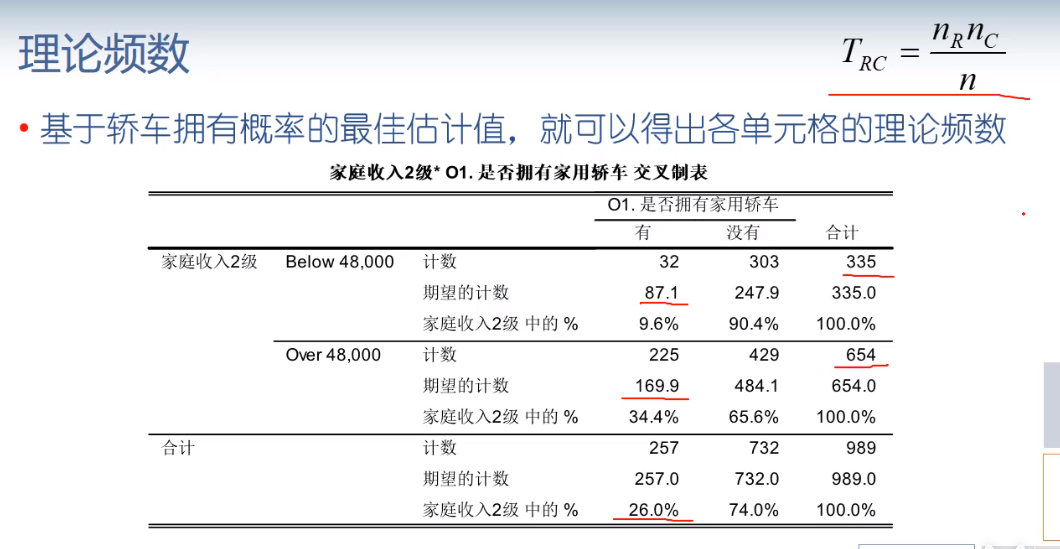
$H_0$ ：观察频数与期望频数没有差别
其原理为考察基于 $H_0$ 的理论频数分布和实际频数分布间的差异大小，据此求出相应的P值
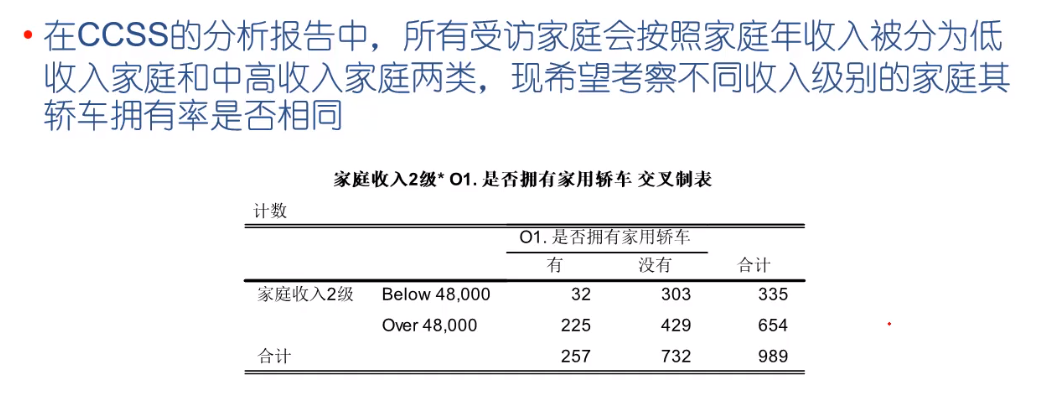
分析实例

残差平方和
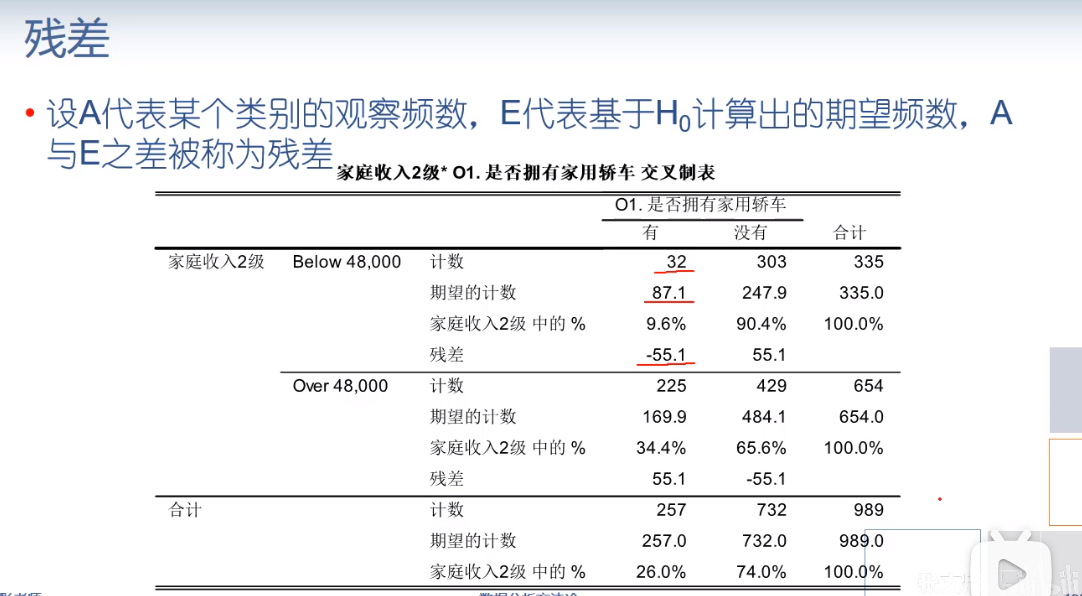
- 残差可以表示某一个单元格中观察值和理论值的偏离程度
- 但残差有正有负，相加后会彼此抵消，总和仍然为0
- 为此可以将残差平方后求和，以表示样本总的偏离无效假设的程度
卡方统计量
- 另一方面，残差大小是一个相对的概念
  - 相对于期望频数为10时，20的残差非常大
  - 相对于期望频数为1000时，20的残差就很小
- 因此又将残差平方除以期望频数再求和，以标准化观察频数与期望频数的差别
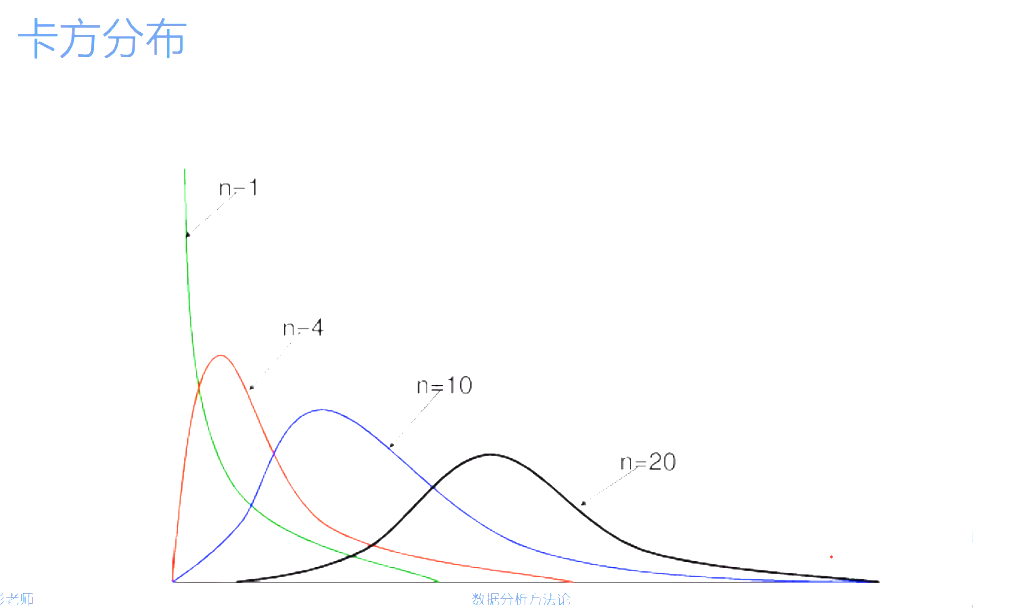
  - 这就是卡方统计量，在1990年由英国统计学家Pearson首次提出
$X^2=\sum{\frac{(A-E)^2}{E}}=\sum_{i=1}^{k}{\frac{(A_i-E_i)^2}{E_i}}=\sum_{i=1}^{k}{\frac{(A_i-np_i)^2}{np_i}}\cdots (i=1,2,3,L\ \ k)$
- 当观察频数与期望频数完全一致时，卡方值为0
- 观察频数与期望频数越接近，两者之间的差异越小，卡方值越小
- 反之，观察频数与期望频数差别越大，两者之间的差异越大，卡方值越大
- 当然，卡方值的大小也和自由度有关

4.9 如何正确选择统计分析方法

4.9.1 确定假设检验方法的两大要素

研究设计
- 成组设计：比较男性和女性对某电影的评分
- 配对设计/配伍设计：受试者在三种候选包装中选择最满意的一种
- 更加复杂的试验设计：拉丁方设计、均匀设计等
变量类型
- 连续变量：两种促销方式的销量比较
- 有序变量：评价结果为优良中差的比较
- 无序变量：不同学校的毕业生择业去向比较

4.9.2 对自身总体进行推断

连续变量：单变量t检验
- 新样品评分是否达到基本要求
无序分类变量：二项分布、卡方分布检验
- 筛子分布是否均匀
- 性别比例是否为假定的数值
有序分类变量：秩和检验
- 成绩优良中差的分布是否符合假定情况

4.9.3 因变量：连续

单个自变量：二分类 t检验
- 成组t检验促销活动对销量有无作用
- 配对t检验培训前后销售额的比较
单个自变量：多分类单因素方差分析
- 三种促销方式的销量比较
- 后续有两两比较
单个自变量：连续
- 相关分析：考察两变量在数量上的依存关系
- 回归分析：考察一个变量对另一个变量影响程度的大小
多个自变量：分类变量为主方差分析模型
- 便于两两比较
- 有多种图形帮助分析
- 自变量间可能有主次之分
多个自变量：连续变量为主线性回归模型
- 本质上和方差分析等价
- 可利用散点图、回归线等图形帮助解释
- 可用逐步法对自变量进行自动筛选

4.9.3 因变量：有序分类

当分类数较多时，可近似按照连续变量处理
单个自变量
二分类秩和检验
多分类秩和检验
- 后续有两两比较问题
连续 Logistic回归
多个自变量
- Logistic回归
- 判别分析
- 最优尺度分析

4.9.4 因变量：无序分类（含二分类）

单个自变量
- 二分类卡方检验
- 多分类卡方检验
  - 后续有两两比较问题
- 连续没有简单模型
多个自变量：分类变量为主
- Logistic回归分析
- 判别分析
- 最优尺度分析

4.9.5 简单推断方法总结

对连续因变量的统计方法是最全面的
有序分类变量往往都近似的在当做连续性变量处理，或者退化成无序分类变量处理
无序分类因变量一般使用卡方检验，但只能得到粗糙的结果，精细分析困难
复杂的统计模型实际上都是让各种变量在拟合时尽量箱连续性变量靠拢（变量变换、概率评分）

统计分析入门

# 统计分析入门

# 1.1 个体、变量与变异

# 1.1.1 个体

# 1.1.2 变量

# 1.1.3 变异

# 1.2 变量类型

# 1.2.1 连续变量（continuous variable）

# 1.2.2 离散型变量（discrete variable）

# 1.2.3 变量类型：总结

# 1.3 数据类型的转换

# 1.4 总体、样本与随机抽样

# 1.4.1 总体

# 1.4.2 样本

# 1.4.3 随机抽样

# 1.5 统计量、总体参数与抽样误差

# 1.5.1 统计量

# 1.5.2 总体参数

# 1.5.3 抽样误差

# 1.6 频率、概率与小概率事件

# 1.6.1 频率

# 1.6.2 概率

# 1.6.3 小概率事件

# 1.7 统计研究的步骤

# 1.7.1 设计

# 1.7.2 收集

# 1.7.3 整理

# 1.7.4 分析

# 2.统计描述

# 2.1 连续变量和分类变量的统计描述

# 2.1.1 频数表

# 2.1.2 从频数图/表中可获得的信息

# 2.1.3 进一步的统计描述指标

# 2.2 集中趋势的描述指标（Central tendency）

# 2.2.1 均数

# 2.2.1.1 均数

# 2.2.1.2 均数的优点

# 2.2.1.3 均数的缺点

# 2.2.1.4 均数的适用范围

# 2.2.2 中位数

# 2.2.2.1 中位数

# 2.2.2.2 中位数的优点

# 2.2.2.3 中位数的缺点

# 2.2.3 几何均数

# 2.2.4 众数

# 2.2.5 截尾均数

# 2.3 离散趋势的描述指标 Dispersion tendency

# 2.3.1 全距

# 2.3.2 方差

# 2.3.3 标准差

# 2.3.4 变异系数

# 2.3.5 方差-标准差-变异系数的使用范围

# 2.3.6 百分位数

# 2.3.7 四分位数

# 2.3.8 分布形状描述指标

# 2.4 分类变量的常用描述指标

# 2.4.1 比

# 2.4.2 率

# 3.统计推断

# 3.1 从频率分布到概率分布

# 3.2 正态分布

# 3.3 标准正态分布

# 3.4 二项分布

# 3.4.1 基本概念

# 3.4.2 二项分布的基本特征

# 3.5 统计推断

# 3.6 抽样误差与标准误

# 3.6.1 抽样误差

# 3.6.2 中心极限定理

# 3.6.3 标准误

# 3.6.4 影响抽样误差的因素

# 3.6.5 t分布

# 3.6.5.1 t分布

# 3.6.5.2 t分布的图形特征和t界值

# 3.6.5.3 样本率的抽样分布

# 3.7 参数估计

# 3.7.1 推断方法

# 3.7.2 可信区间的计算

# 3.7.3 可信区间的含义

# 4.常用假设检验方法

统计分析入门

1.1 个体、变量与变异

1.1.1 个体

1.1.2 变量

1.1.3 变异

1.2 变量类型

1.2.1 连续变量（continuous variable）

1.2.2 离散型变量（discrete variable）

1.2.3 变量类型：总结

1.3 数据类型的转换

1.4 总体、样本与随机抽样

1.4.1 总体

1.4.2 样本

1.4.3 随机抽样

1.5 统计量、总体参数与抽样误差

1.5.1 统计量

1.5.2 总体参数

1.5.3 抽样误差

1.6 频率、概率与小概率事件

1.6.1 频率

1.6.2 概率

1.6.3 小概率事件

1.7 统计研究的步骤

1.7.1 设计

1.7.2 收集

1.7.3 整理

1.7.4 分析

2.统计描述

2.1 连续变量和分类变量的统计描述

2.1.1 频数表

2.1.2 从频数图/表中可获得的信息

2.1.3 进一步的统计描述指标

2.2 集中趋势的描述指标（Central tendency）

2.2.1 均数

2.2.1.1 均数

2.2.1.2 均数的优点

2.2.1.3 均数的缺点

2.2.1.4 均数的适用范围

2.2.2 中位数

2.2.2.1 中位数

2.2.2.2 中位数的优点

2.2.2.3 中位数的缺点

2.2.3 几何均数

2.2.4 众数

2.2.5 截尾均数

2.3 离散趋势的描述指标 Dispersion tendency

2.3.1 全距

2.3.2 方差

2.3.3 标准差

2.3.4 变异系数

2.3.5 方差-标准差-变异系数的使用范围

2.3.6 百分位数

2.3.7 四分位数

2.3.8 分布形状描述指标

2.4 分类变量的常用描述指标

2.4.1 比

2.4.2 率

3.统计推断

3.1 从频率分布到概率分布

3.2 正态分布

3.3 标准正态分布

3.4 二项分布

3.4.1 基本概念

3.4.2 二项分布的基本特征

3.5 统计推断

3.6 抽样误差与标准误

3.6.1 抽样误差

3.6.2 中心极限定理

3.6.3 标准误

3.6.4 影响抽样误差的因素

3.6.5 t分布

3.6.5.1 t分布

3.6.5.2 t分布的图形特征和t界值

3.6.5.3 样本率的抽样分布

3.7 参数估计

3.7.1 推断方法

3.7.2 可信区间的计算

3.7.3 可信区间的含义

4.常用假设检验方法

4.1 为什么要做检验